We study in detail the solution of a basic strongly correlated model,namely, the dimer Hubbard model. This model is the simplest realization of a cluster DMFT problem.

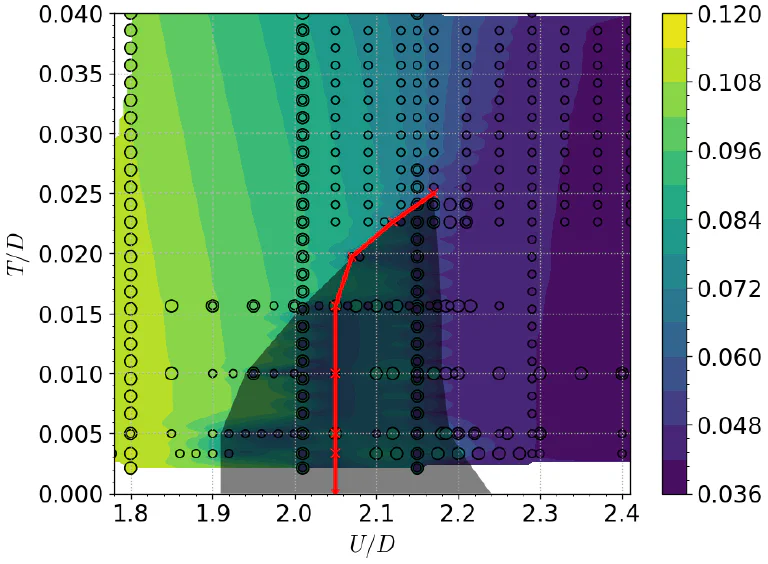
We provide a detailed description of the solutions in the “coexistent region” where two (meta)stable states of the DMFT equations are found, one a metal and the other an insulator. Moreover, we describe in detail how these states break down at their respective critical lines. We clarify the key role played by the intra-dimer correlation, which here acts in addition to the onsite Coulomb correlations.

We review the important issue of the Mott-Peierls insulator crossover where we characterize a variety of physical regimes. In a subtle change in the electronic structure the Hubbard bands evolve from purely incoherent(Mott) to purely coherent (Peierls) through a state with unexpected mixed character. We find a singlet pairing temperature \(T^*\) below which the localized electrons at each atomic site can bind into a singlet and quench their entropy, this uncovers a new paradigm of a para-magnetic Mott insulator.

Finally, we discuss the relevance of our results for the interpretation of various experimental studies in VO\(_2\). We present a variety of arguments that allow us to advance the conclusion that the long-lived (meta-stable)metallic phase, induced in pump-probe experiments, and the thermally activated M\(_1\) meta-stable metallic state in nano-domains are the same. In fact, they may all be qualitatively described by the dimerized correlated metal state of our model.